Uncertainty Visualization¶

Be able to visualize uncertainty is often neglected but it is a challenging topic. Depending on the number of input parameters and the dimension of the quantitie of interest, there are several options implemented in the package.

Function or class	Dimensionality		Description
Function or class	Input \| Output		Description
`doe.doe()`	n-scalar	scalar, vector	Design of Experiment
`doe.response_surface()`	<5 scalar	scalar, vector	Response surface (fig or movies)
`hdr.HdrBoxplot`	vector	vector	Median realization with PCA
`kiviat.Kiviat3D`	>3 scalar	scalar, vector	3D version of the radar/spider plot
`uncertainty.pdf()`		scalar, vector	Output PDF
`uncertainty.corr_cov()`	scalar	vector	Correlation of the inputs and outputs
`uncertainty.sobol()`	scalar	scalar, vector	Sensitivity indices

All options return a figure object that can be reuse using reshow(). This enables some modification of the graph. In most cases, the first parameter data is of shape (n_samples, n_features).

Response surface¶

What is it?¶

A response surface can be created to visualize the surrogate model as a function of two input parameters, the surface itself being colored by the value of the function. The response surface is automatically plotted when requesting uncertainty quantification if the number of input parameters is less than 5. For a larger number of input parameters, a Kiviat-3D graph is plotted instead (see Kiviat 3D section).

If only 1 input parameter is involved, the response surface reduces to a response function. The default display is the following:

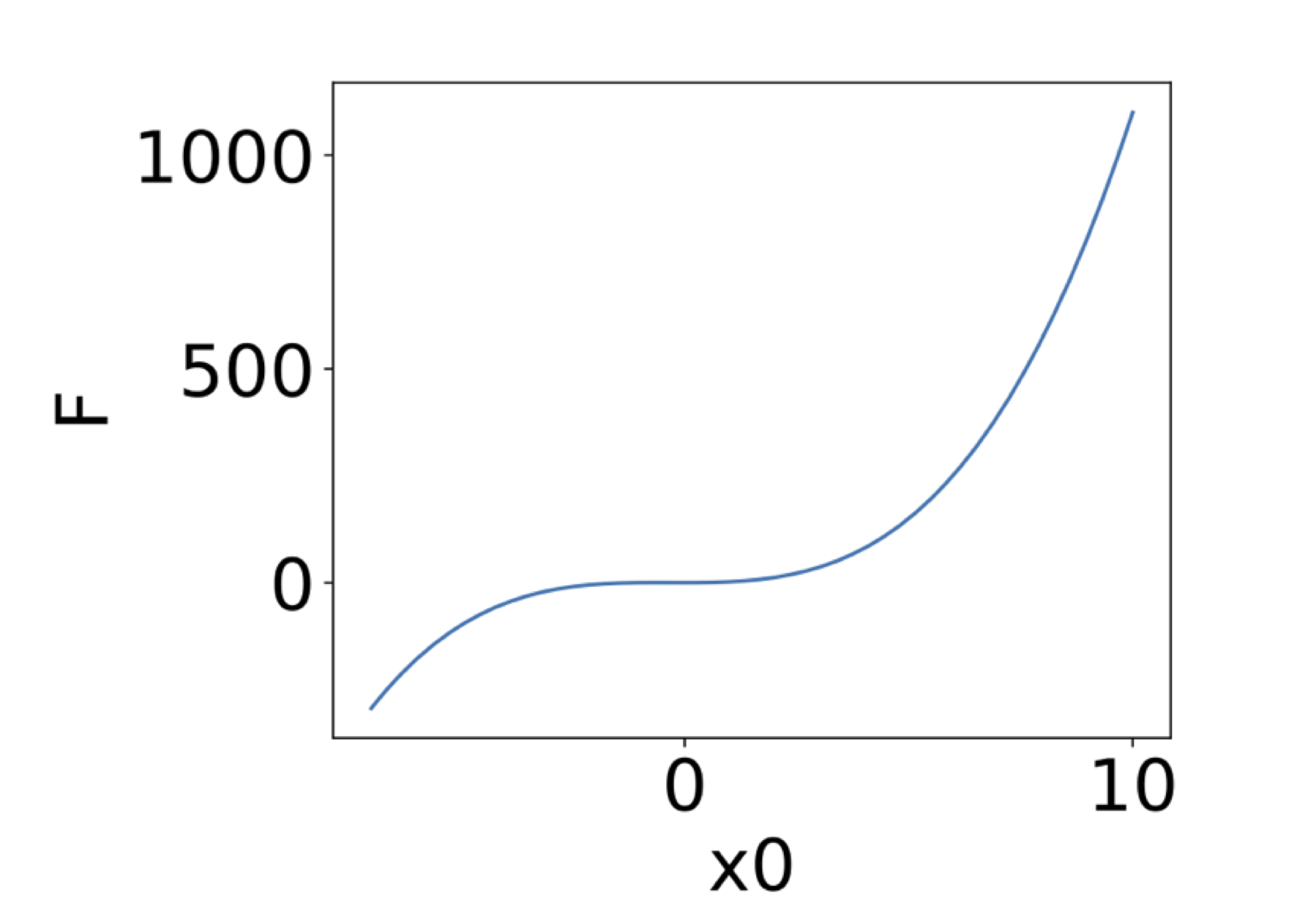
If exactly 2 input parameters are involved, it is possible to generate the response surface, the surface itself being colored by the value of the function. The corresponding values of the 2 input parameters are displayed on the x and y axis, with the following default display:

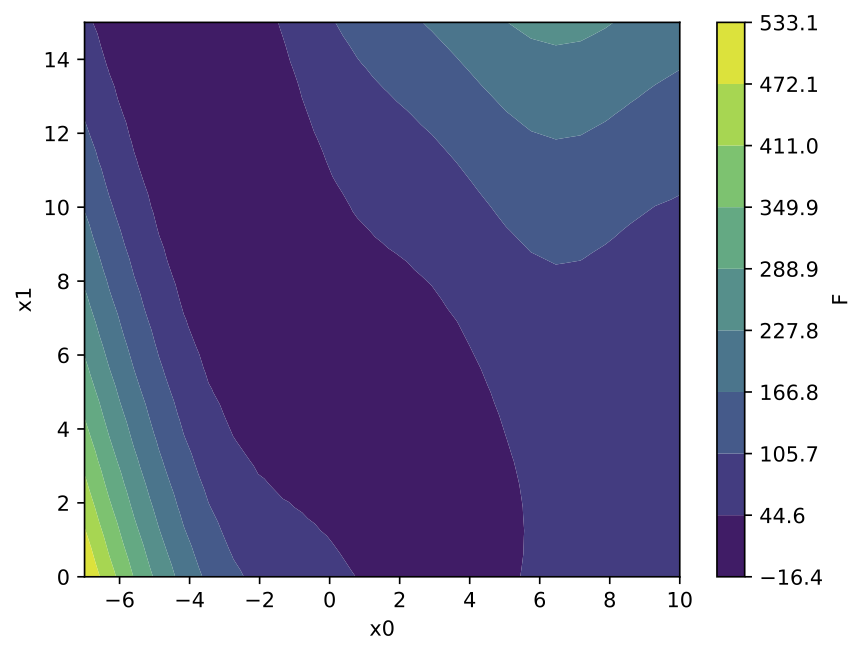
Because the response surface is a 2D picture, a set of response surfaces is generated when dealing with 3 input parameters. The value of the 3rd input parameter is fixed to a different value on each plot. The obtained set of pictures is concatenated to one single movie file in mp4 format:

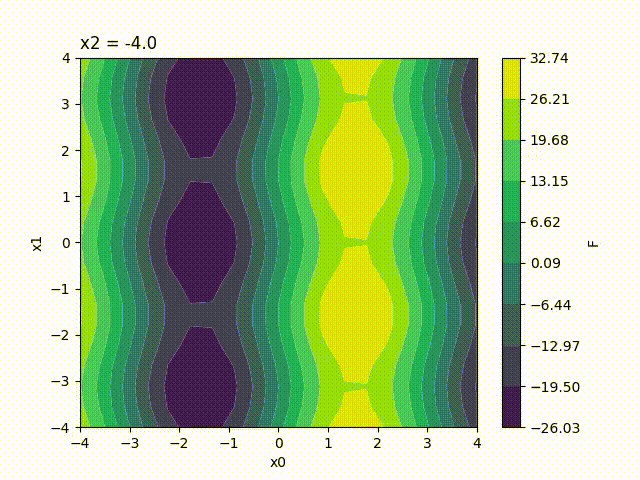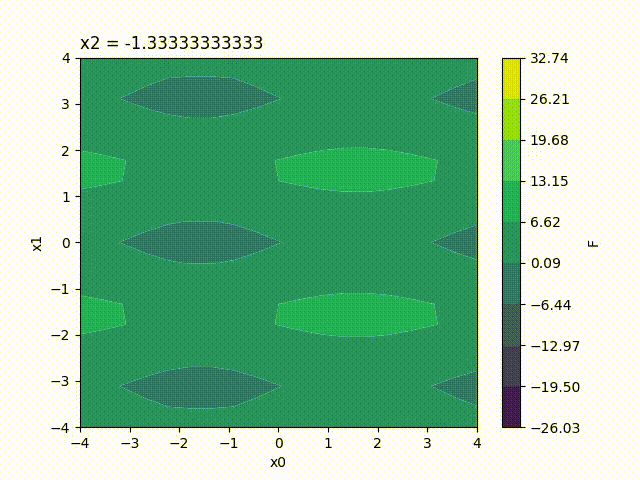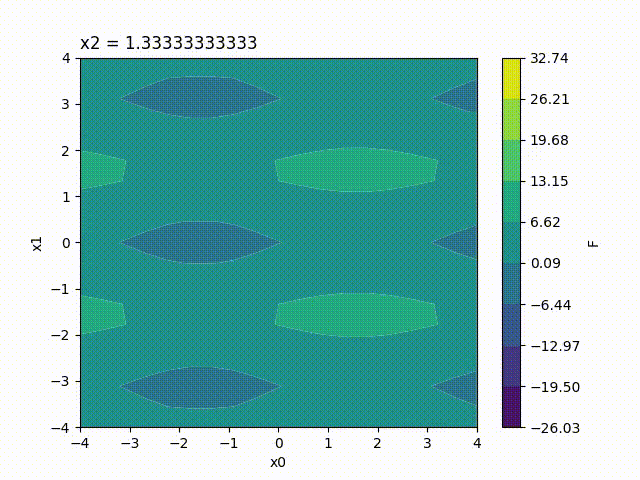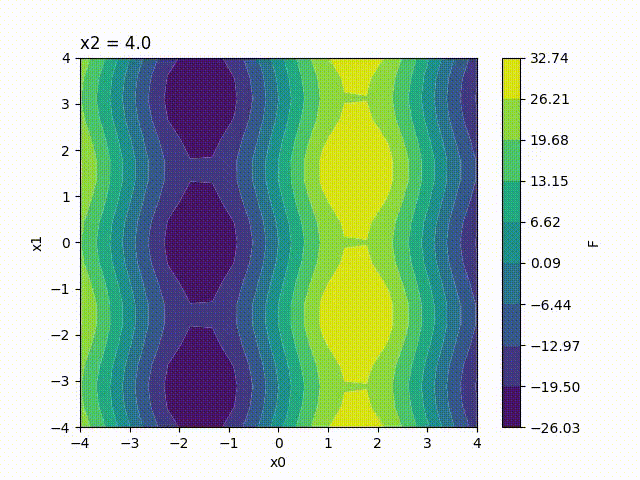
Finally, response surfaces can also be plotted for 4 input parameters. A set of several movies is created, the value of the 4th parameter being fixed to a different value on each movie.

Options¶

Several display options can be set by the user to modify the created response surface. All the available options are listed in the following table:

Option name	Dimensionality	Default	Description
Option name	Dimensionality	Default	Description
doe	Array-like.	None	Display the Design of Experiment on graph, represented by black dots.
resampling	Integer.	None	Display the n last DoE points in red to easily identify the resampling.
xdata	List of real numbers. Size = length of the output vector.	If output is a scalar: None If output is a vector: regular discretisation between 0 and 1	Only used if the output is a vector. Specify the discretisation of the output vector for 1D response function and for integration of the output before plotting 2D response function.
axis_disc	List of integers. One value per parameter.	50 in 1D 25,25 in 2D 20,20,20 in 3D 15,15,15,15 in 4D	Discretisation of the response surface on each axis. Values of the 1st and 2nd parameters influence the resolution, values for the 3rd and 4th parameters influence the number of frame per movie and the movie number respectively.
flabel	String.	‘F’	Name of the output function.
plabels	List of string. One chain per parameter.	‘x0’ for 1st dim ‘x1’ for 2nd dim ‘x2’ for 3rd dim ‘x3’ for 4th dim	Name of the input parameters to be on each axis.
feat_order	List of integers. One value per parameter.	1 in 1D 1,2 in 2D 1,2,3 in 3D 1,2,3,4 in 4D	Axis on which each parameter should be plotted. The parameter in 1st position is plotted on the x-axis and so on… All integer values from 1 to the total dimension number should be specified.
ticks_nbr	Integer.	10	Number of ticks in the colorbar.
range_cbar	List of real numbers. Two values.	Minimal and maximal values in output data	Minimal and maximal values in the colorbar. Output values that are out of this scope are plotted in white.
contours	List of real numbers.	None	Values of the iso-contours to plot.
fname	String.	‘Response_surface .pdf’	Name of the response surface file(s). Can be followed by an additional int.

Example¶

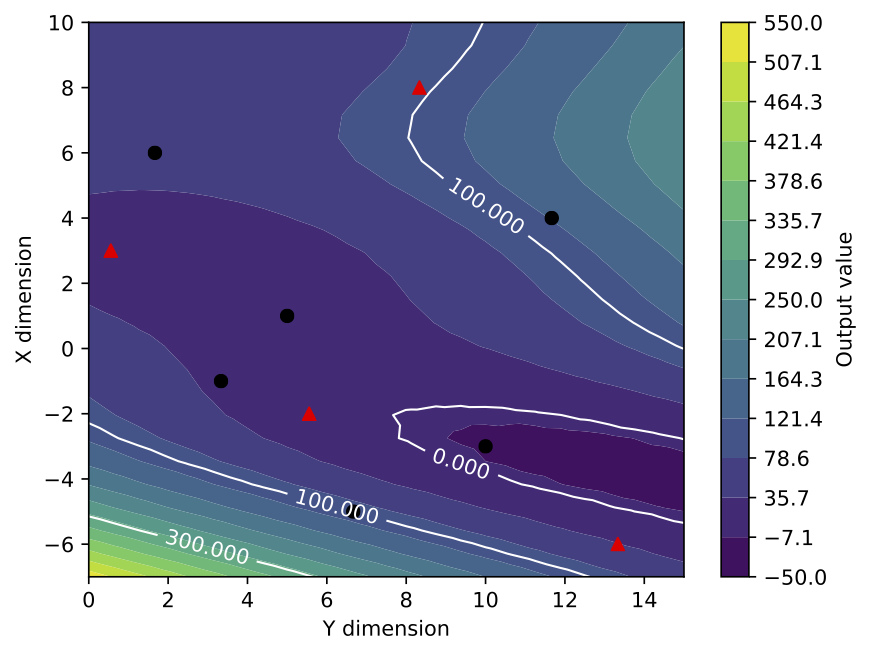
As an example, the previous response surface for 2 input parameters is now plotted with its design of experiment, 4 of the points being indicated as a later resampling (4 red triangles amongs the black dots). Additional iso-contours are added to the graph and the axis corresponding the each input parameters are interverted. Note also the new minimal and maximal values in the colorbar and the increased color number. Finally, the names of the input parameters and of the cost function are also modified for more explicit ones.

HDR-Boxplot¶

What is it?¶

This implements an extension of the highest density region boxplot technique [Hyndman2009]. When you have functional data, which is to say: a curve, you will want to answer some questions such as:

What is the median curve?
Can I draw a confidence interval?
Or, is there any outliers?

This module allows you to do exactly this:

data = np.loadtxt('data/elnino.dat')
print('Data shape: ', data.shape)

hdr = batman.visualization.HdrBoxplot(data)
hdr.plot()

The output is the following figure:

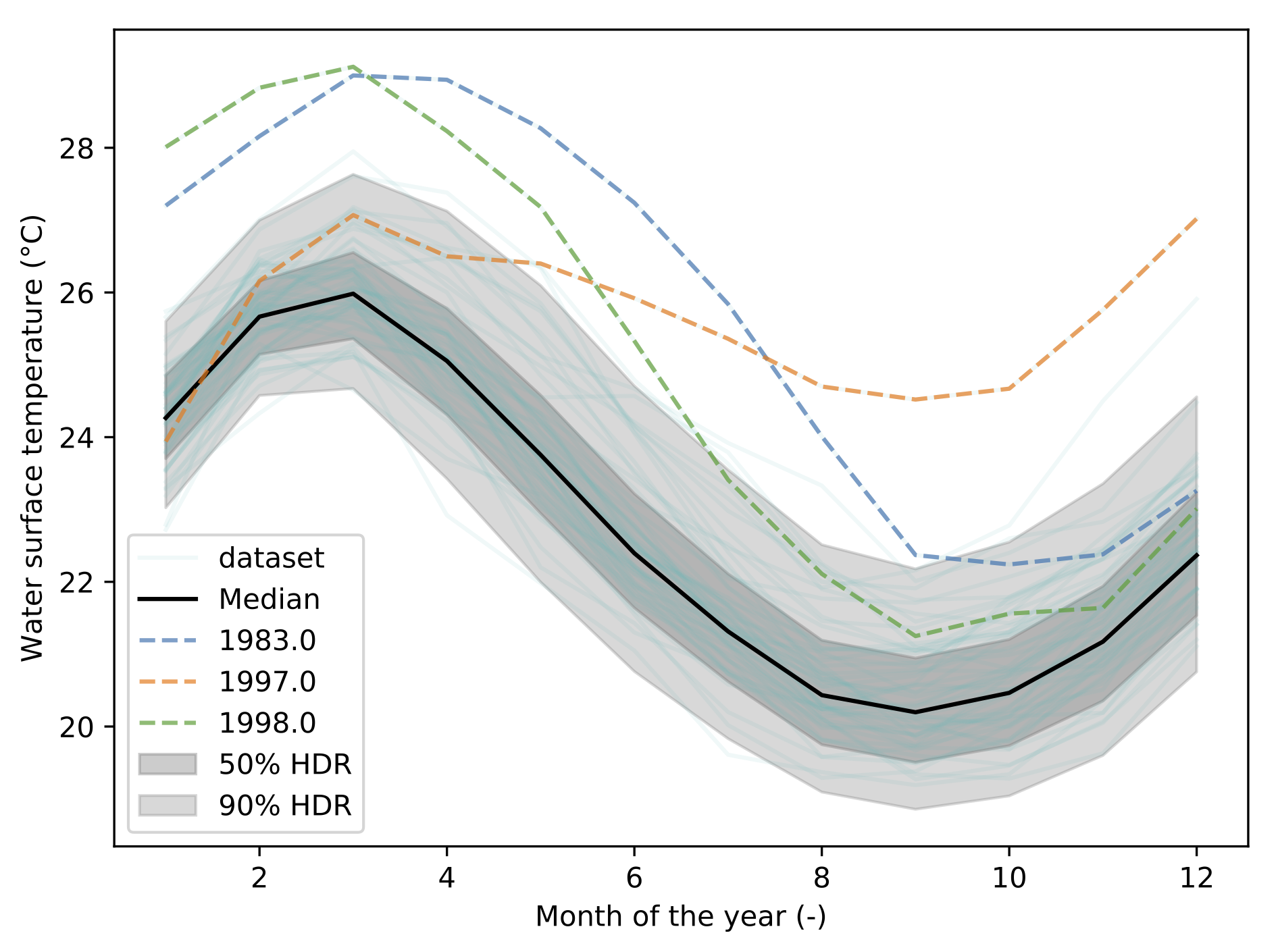
How does it work?¶

Behind the scene, the dataset is represented as a matrix. Each line corresponding to a 1D curve. This matrix is then decomposed using Principal Components Analysis (PCA). This allows to represent the data using a finit number of modes, or components. This compression process allows to turn the functional representation into a scalar representation of the matrix. In other words, you can visualize each curve from its components. With 2 components, this is called a bivariate plot:

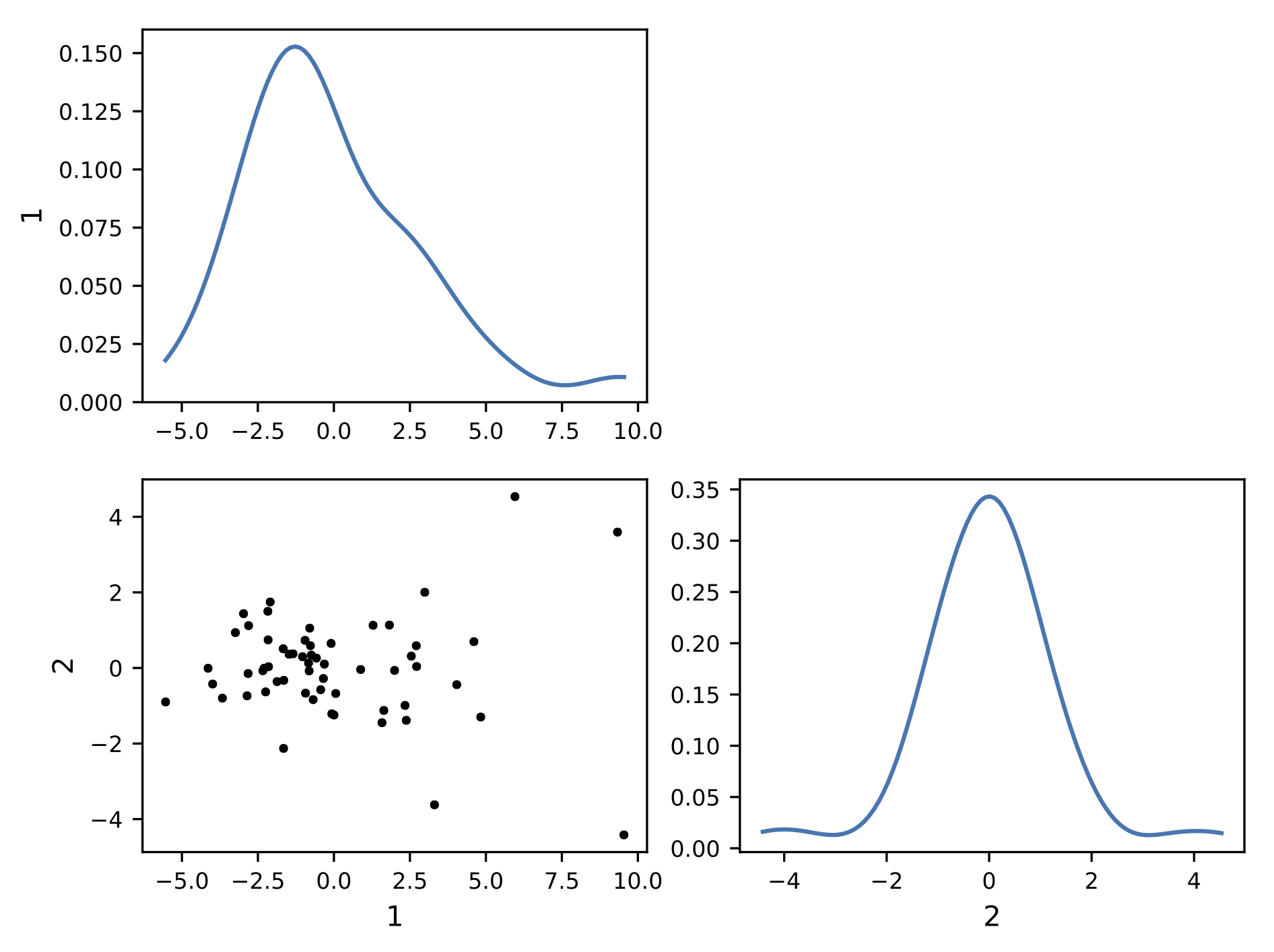
This visualization exhibit a cluster of points. It indicate that a lot of curve lead to common components. The center of the cluster is the mediane curve. An the more you get away from the cluster, the more the curve is unlikely to be similar to the other curves.

Using a kernel smoothing technique (see PDF), the probability density function (PDF) of the multivariate space can be recover. From this PDF, it is possible to compute the density probability linked to the cluster and plot its contours.

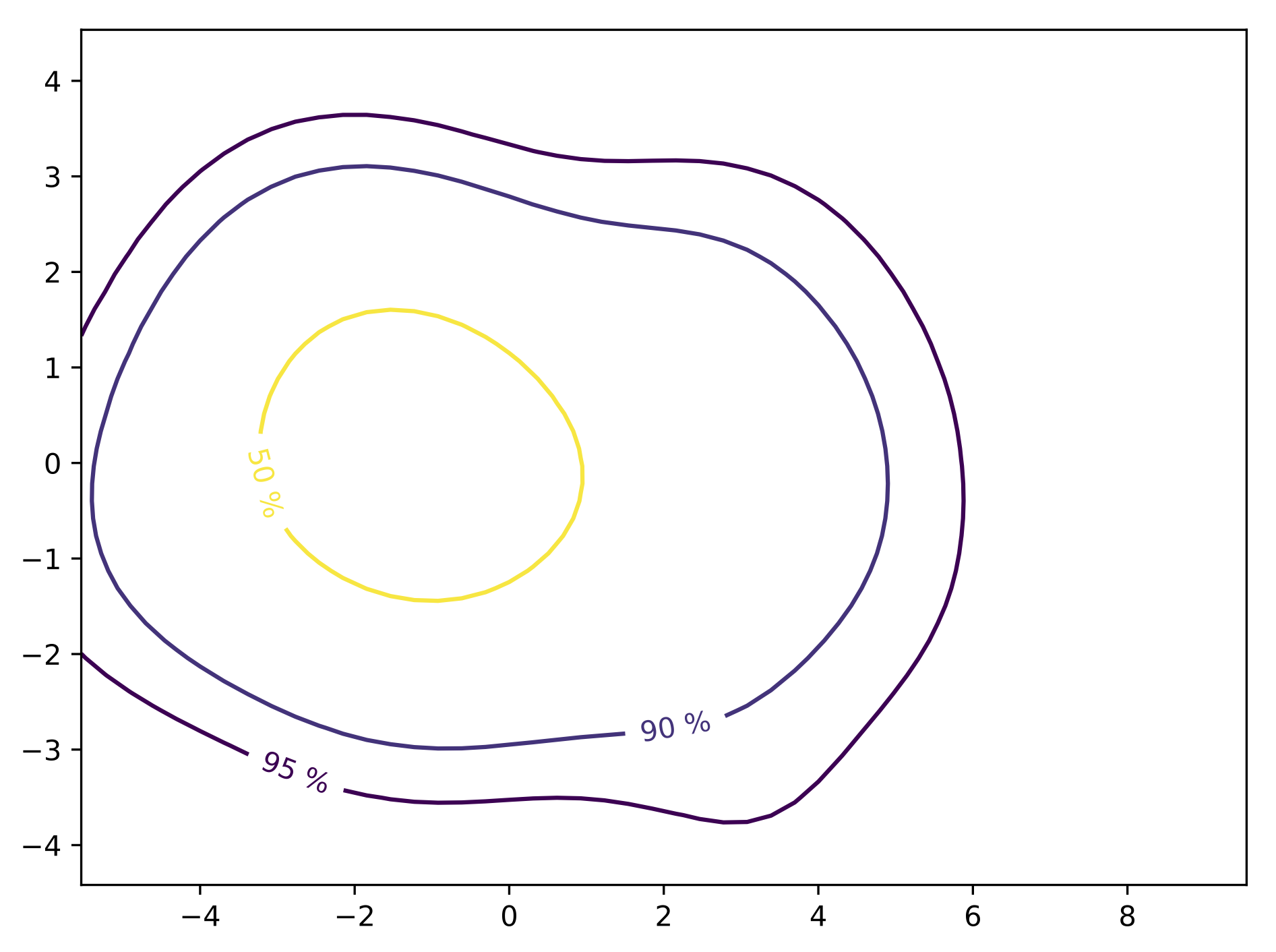
Finally, using these contours, the different quantiles are extracted allong with the mediane curve and the outliers.

Uncertainty visualization¶

Appart from these plots. It implements a technique called Hypothetical Outcome plots (HOPs) [Hullman2015] and extend this concept to functional data. Using the HDR Boxplot, each single realisation is superposed. All these frames are then assembled into a movie. The net benefit is to be able to observe the spatial/temporal correlations. Indeed, having the median curve and some intervals does not indicate how each realisation are drawn, if there are particular patterns. This animated representation helps such analysis:

hdr.f_hops()

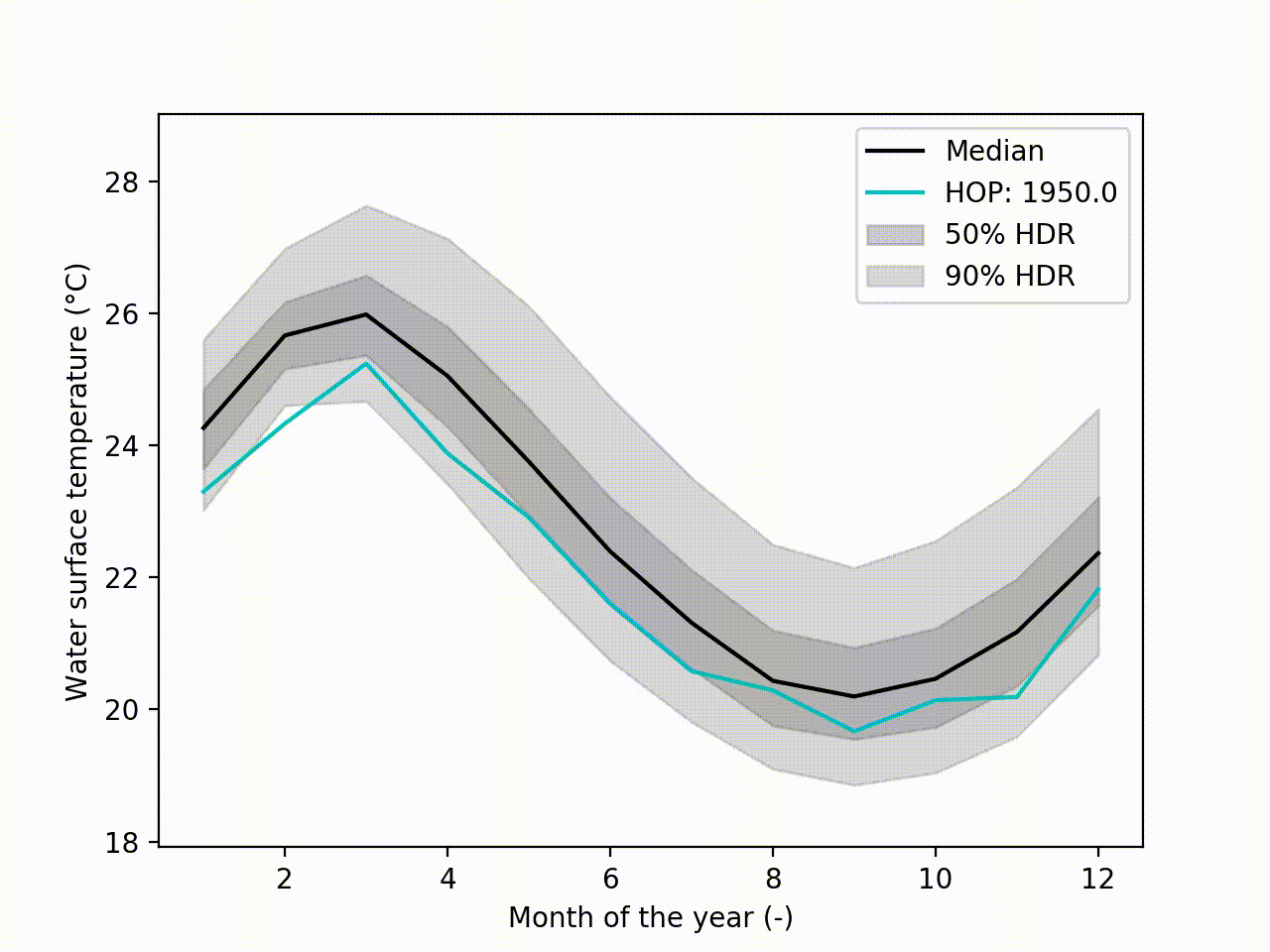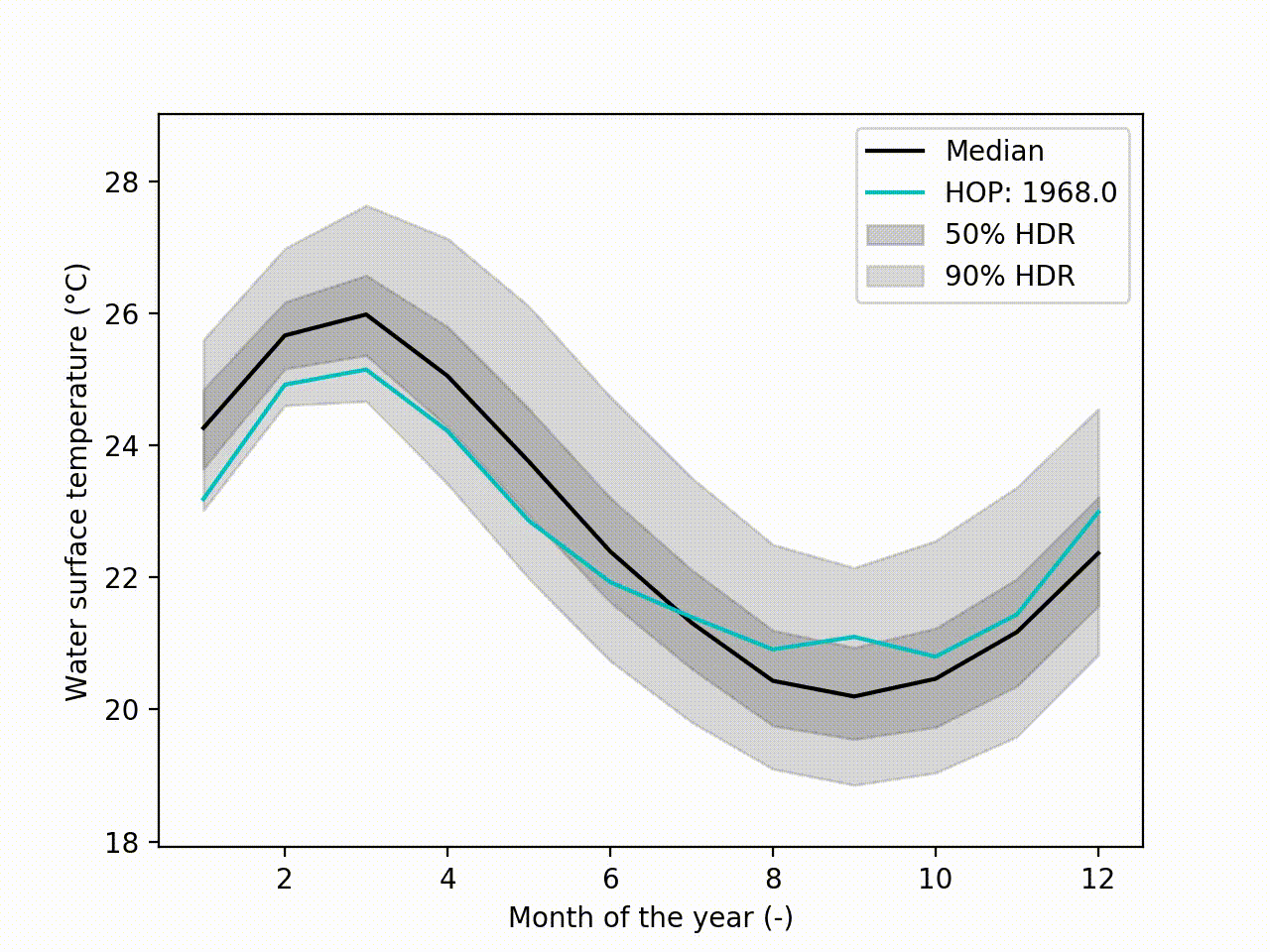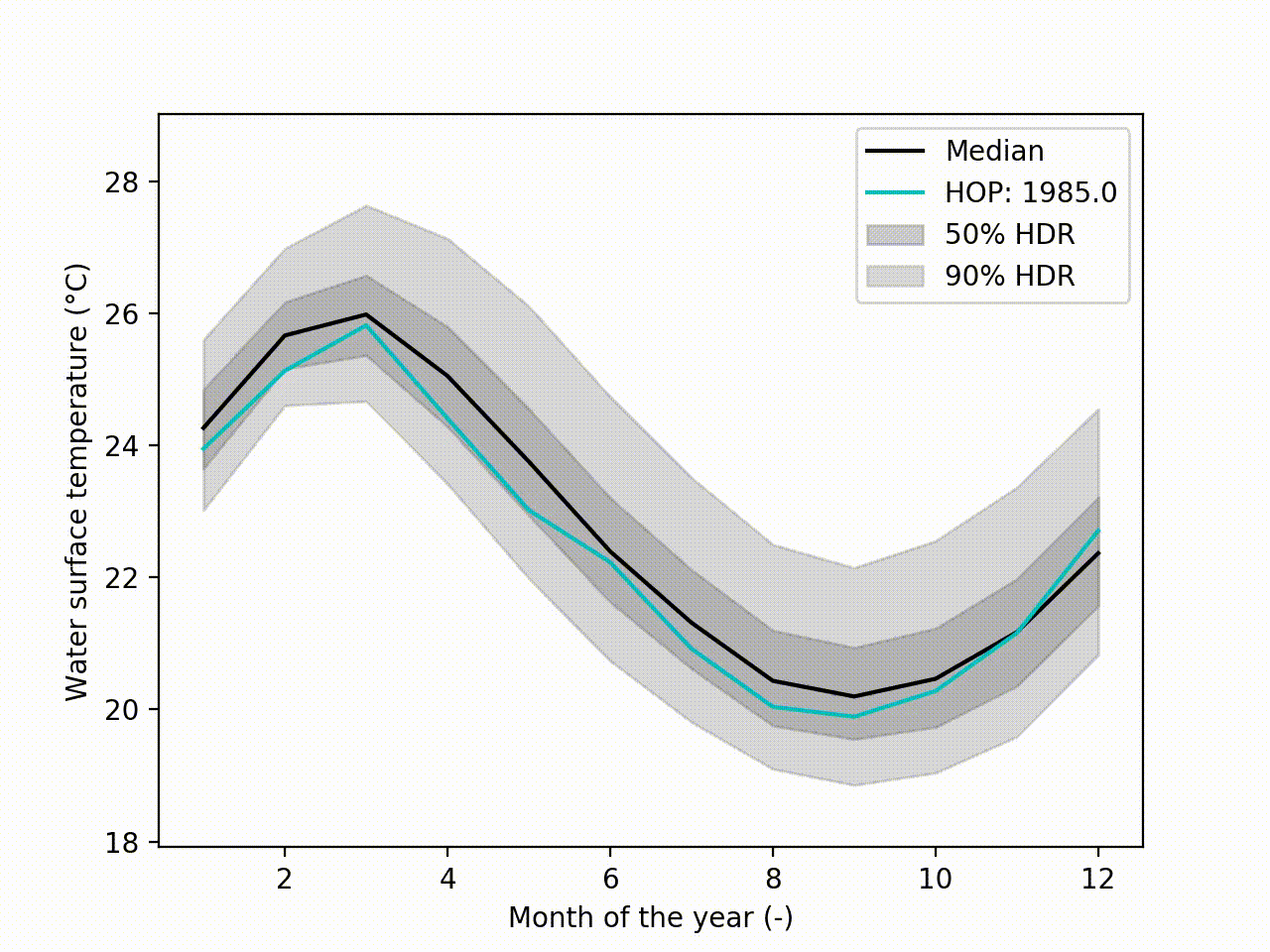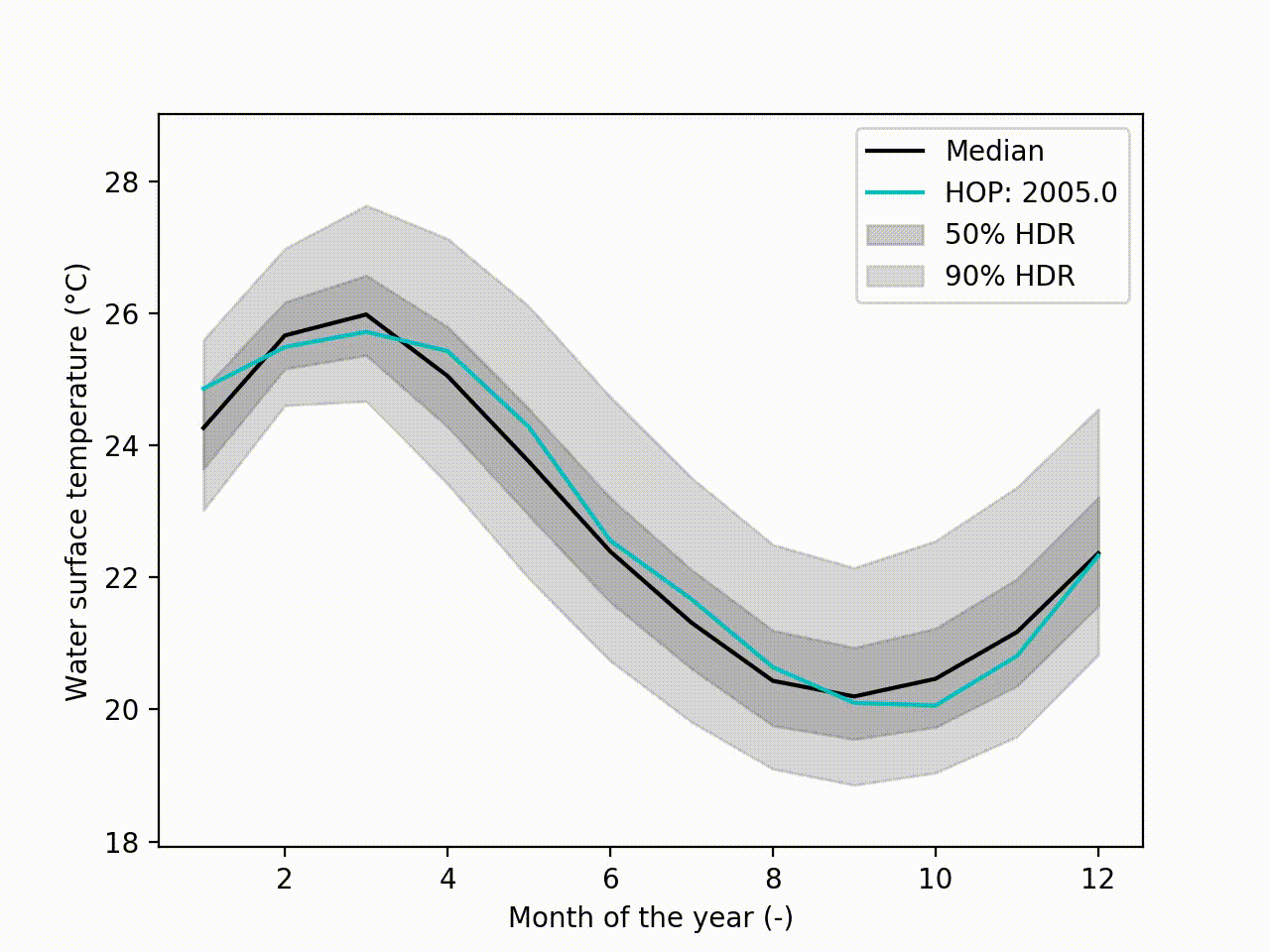
Another possibility is to visualize the outcomes with sounds. Each curve is mapped to a series of tones to create a song. Combined to the previous f-HOPs this opens a new way of looking at data:

hdr.sound()

Note

The hdr.sound() output is an audio wav file. A combined video can be obtain with ffmpeg:

ffmpeg -i f-HOPs.mp4 -i song-fHOPs.wav mux_f-HOPs.mp4

The gif is obtain using:

ffmpeg -i f-HOPs.mp4 -pix_fmt rgb8 -r 1 data/f-HOPs.gif

Kiviat 3D¶

The HDR technique is usefull for visualizing functional output but it does not give any information on the input parameter used. Radar plot or Kiviat plot can be used for this purpose. A single realisation can be seen as a 2D kiviat plot which different axes each represent a given parameter. The surface itself being colored by the value of the function.

To be able to get a whole set of sample, a 3D version of the Kiviat plot is used [Hackstadt1994]. Thus, each sample corresponds to a 2D Kiviat plot:

kiviat = batman.visualization.Kiviat3D(space, bounds, feval, param_names)
kiviat.plot()

When dealing with functional output, the color of the surface does not gives all the information on a sample as it can only display a single information: the median value in this case. Hence, the proposed approach is to combine a functional-HOPs-Kiviat with sound:

batman.visualization.kiviat.f_hops(fname=os.path.join(tmp, 'kiviat.mp4'))
hdr = batman.visualization.HdrBoxplot(feval)
hdr.sound()

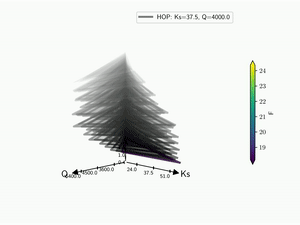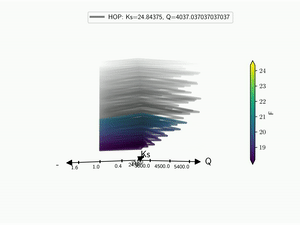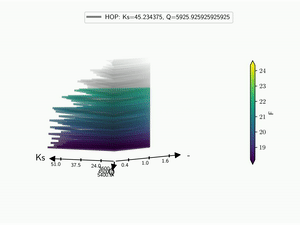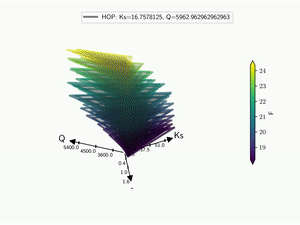
Probability Density Function¶

A multivariate kernel density estimation [Wand1995] technique is used to find the probability density function (PDF) \(\hat{f}(\mathbf{x_r})\) of the multivariate space. This density estimator is given by

\[\hat{f}(\mathbf{x_r}) = \frac{1}{N_{s}}\sum_{i=1}^{N_{s}} K_{h_i}(\mathbf{x_r}-\mathbf{x_r}_i),\]

With \(h_{i}\) the bandwidth for the i th component and \(K_{h_i}(.) = K(./h_i)/h_i\) the kernel which is chosen as a modal probability density function that is symmetric about zero. Also, \(K\) is the Gaussian kernel and \(h_{i}\) are optimized on the data.

So taking a case with a functionnal output [Roy2017], we can recover its PDF with:

fig_pdf = batman.visualization.pdf(data)

Correlation matrix¶

The correlation and covariance matrices are also availlable:

batman.visualization.corr_cov(data, sample, func.x, plabels=['Ks', 'Q'])

Sobol’¶

Once Sobol’ indices are computed , it is easy to plot them with:

indices = [s_first, s_total]
batman.visualization.sobol(indices, p_lst=['Tu', r'$\alpha$'])

In case of functionnal data [Roy2017b], both aggregated and map indices can be passed to the function and both plot are made:

indices = [s_first, s_total, s_first_full, s_total_full]
batman.visualization.sobol(indices, p_lst=['Tu', r'$\alpha$'], xdata=x)

References¶

Hyndman2009: Rob J. Hyndman and Han Lin Shang. Rainbow plots, bagplots and boxplots for functional data. Journal of Computational and Graphical Statistics, 19:29-45, 2009
Hullman2015: Jessica Hullman and Paul Resnick and Eytan Adar. Hypothetical Outcome Plots Outperform Error Bars and Violin Plots for Inferences About Reliability of Variable Ordering. PLoS ONE 10(11): e0142444. 2015. DOI: 10.1371/journal.pone.0142444
Hackstadt1994: Steven T. Hackstadt and Allen D. Malony and Bernd Mohr. Scalable Performance Visualization for Data-Parallel Programs. IEEE. 1994. DOI: 10.1109/SHPCC.1994.296663
Wand1995: M.P. Wand and M.C. Jones. Kernel Smoothing. 1995. DOI: 10.1007/978-1-4899-4493-1
Roy2017b: P.T. Roy et al.: Comparison of Polynomial Chaos and Gaussian Process surrogates for uncertainty quantification and correlation estimation of spatially distributed open-channel steady flows. SERRA. 2017. DOI: 10.1007/s00477-017-1470-4

Acknowledgement¶

We are gratefull to the help and support on OpenTURNS Michaël Baudin has provided.